PROIEZIONI ORTOGONALI
IN QUESTA SEZIONE POTRETE LEGGERE E SCARICARE:
1) SPIEGAZIONI DETTAGLIATE
2) DISEGNI ESPLICATIVI
3) APPUNTI COMPLETI
...RELATIVI A TUTTI GLI ARGOMENTI DELLE PROIEZIONI ORTOGONALI NORMALMENTE AFFRONTATI IN UN CORSO DI DISEGNO TECNICO.
MATERIALE QUESTO UTILISSIMO SIA PER GLI STUDENTI UNIVERSITARI SIA PER GLI STUDENTI DELLA SCUOLA SUPERIORE.
AD OGNI ARGOMENTO E' DEDICATA UNA SPECIFICA PAGINA. PER ACCEDERE AI VARI ARGOMENTI/ PAGINE E' SUFFICIENTE CLICCARE SULLE VOCI CHE COMPAIONO NEL MENU A DISCESA VISIBILE POGGIANDO IL MOUSE SULLA PAROLA "PROIEZIONI ORTOGONALI" CHE COMPARE IN TESTATA.
IL MENU A DISCESA VIENE ANCHE A COSTITUIRE UN ELENCO DI TUTTI GLI ARGOMENTI TRATTATI, UNA SORTA DI "PROGRAMMA DEL CORSO".
RIPETIZIONI DI DISEGNO TECNICO
INVIANDO UNA E-MAIL ALLA PAGINA DEI CONTATTI DEL SITO, E' POSSIBILE INFORMARSI PER RICEVERE RIPETIZIONI DI DISEGNO TECNICO: TARIFFE E MODALITA' DI SVOLGIMENTO DELLE LEZIONI.
INTRODUZIONE ALLE PROIEZIONI ORTOGONALI

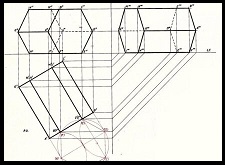
Le Proiezioni Ortogonali sono una tecnica di rappresentazione del Disegno Tecnico, e possono essere esguire a mano (disegno a spolvero) o con l'ausilio di sofware (C.A.D. Computer Aided Design).
L'oggetto viene rappresentato su tre piani di proiezioni perpendicolari tra loro, che ne mostrano tre viste differenti: dall'alto, di fronte e di fianco. L'immagine dell'oggetto che ne deriva è bidimensionale, in scala e quotata (cioè con l’indicazione delle misure).
Non è raro, specialmente nel disegno architettonico, eseguire anche delle rappresentazioni in Proiezioni Ortogonali "sezionate" (cioè come se l’oggetto venisse tagliato da un piano), che ne mostrano l'interno.
COME ESEGUIRE LE PROIEZIONI ORTOGONALI
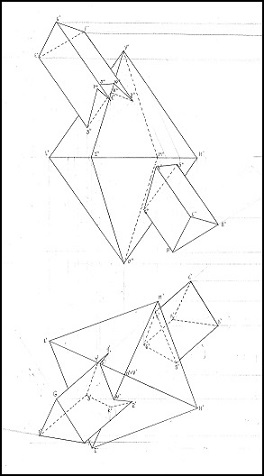
Realizzare le Proiezioni Ortogonali di un oggetto è un procedimento tutto sommato semplice.
La prima cosa da fare è squadrare il foglio da disegno (cioè realizzarne la cornice), anche se tale squadratura non è prevista per le tavole universitarie.
Il foglio da disegno andrà poi diviso in quattro quadranti (cioè in quattro parti) non necessariamente di uguale grandezza, attraverso due linee: una orizzontale (la linea di terra L.T.) e una verticale (la linea t). I quattro quadranti corrispondono a quattro piani, tre dei quali vengono utilizzati per rappresentare le varie viste dell'oggetto sul foglio di lavoro.
Il primo quadrante (in alto a sinistra) corrisponde al piano verticale (P.V.) su cui si rappresenta l'oggetto visto di fronte. Il secondo quadrante (in alto a destra) corrisponde al piano laterale (P.L.) su cui si rappresenta l'oggetto visto di fianco. Il terzo quadrante (in basso a sinistra) corrisponde al piano orizzontale (P.O.) su cui si rappresenta l'oggetto visto dall'alto.
Nella progettazione edilizia, dove le Proiezioni Ortogonali hanno frequentissima utilizzazione, la vista dall’alto dell'edificio (che non comprende il tetto di copertura) si chiama “pianta”. La vista di fronte (cioè la facciata dell'edificio) si chiama “prospetto”. Le viste di fianco, qualora previste, si chiamano "prospetti laterali".
Il quarto quadrante (in basso a destra) è invece quello su cui si esegue la rotazione del piano orizzontale e del piano laterale, attraverso linee tracciate con il compasso o inclinate a 45°.
Le tre viste sono unite tra loro da rette di richiamo, cioè linee parallele che riportano le dimensioni dell'oggetto da un piano di proiezione all’altro. Le rette di richiamo sono le linee di costruzione più importanti del disegno. Come tutte le linee di costruzione, esse vanno tracciate con linea continua e sottile.
I tre quadranti vanno dunque a costituire tre piani di proiezione, che, uniti spazialmente tra loro, definiscono il triedro di proiezione dentro cui si trova l'oggetto nello spazio.
Una volta disegnate le tre viste dell'oggetto, gli spigoli non visibili vanno tracciati con linea marcata ma tratteggiata. Le linee immaginarie invece, quali ad esempio gli assi dei solidi, andranno tracciate con un leggero tratteggio linea-punto.
Se l’oggetto presenta delle rientranze o cavità (cosa frequente nei pezzi meccanici), è possibile mostrane l'interno in Proiezioni Ortogonali tramite delle sezioni. Le sezioni sono viste interne dell’oggetto, immaginando che questo sia tagliato da un piano (solitamente orizzontale o verticale) che lo attraversa. La superficie di sezione viene poi colorata o tratteggiata con segni inclinati di 45° a distanza costante.
Alcuni disegni presentano anche la quotatura, cioè l'indicazione delle dimensioni o delle distanze dell'oggetto dai piani di proiezione. La quotatura comprende lineedi misura (esterne alla figura, parallele alle facce dell'oggetto), valori numerici, frecce terminali e linee di riferimento.
Le quote sono espresse in millimetri e allineate alla direzione delle frecce.
E’ inoltre consigliabile utilizzare il minimo numero indispensabile di quote, per evitare di appesantire troppo il disegno.
TAVOLE SVOLTE SULLE PROIEZIONI ORTOGONALI
NEL BLOG DEL SITO "ALICE APPUNTI" SONO RIPORTATE TANTE TAVOLE SVOLTE, REALIZZATE PASSO PASSO E SPIEGATE PUNTO PER PUNTO.
DA NON PERDERE PER CHIUNQUE STIA PREPARANDO L'ESAME DI DISEGNO TECNICO!
CLICCATE SULLA SOTTOSTANTE ICONA PER ACCEDERE ALLA PAGINA!







