ISCRIVITI AL MIO CANALE YOUTUBE: TROVERAI TUTTO SU COME ESEGUIRE L'ASSONOMETRIA!
ASSONOMETRIA - INTRODUZIONE
L’Assonometria nasce nel XVI secolo per esigenze militari. E' una delle tre principali tecniche di rappresentazione del Disegno Tecnico, insieme alle Proiezioni Ortogonali e alla Prospettiva.
E' una tecnica di rappresentazione molto utilizzata sia in Ingegneria sia in Architettura, e soprattutto nella progettazione di impianti tecnici ed elementi meccanici. Ma anche nella comunicazione visiva.
Questo perchè permette di rappresentare gli oggetti conservando inalterati i rapporti angolari e dimensionali, e fornisce un'unica immagine tridimensionale facilmente comprensibile.
Il nome Assonometria deriva dal fatto che le linee che definiscono l'oggetto rappresentato sono parallele tra loro, secondo tre direzioni stabilite da tre assi ortogonali: l'asse x (per la larghezza), l'asse z (per l'altezza) e l'asse y (per la profondità). Sempre su tali assi sono riportate le misure dell'oggetto rappresentato.
ASSONOMETRIA - PROIEZIONI ASSONOMETRICHE
Le Proiezioni Assonometriche sono, come le Proiezioni Ortogonali, delle proiezioni parallele.
A differenza delle Proiezioni Ortogonali, però, le Proiezioni Assonometriche forniscono immagini più semplici da capire, con una più esplicita tridimensionalità.
In questo tipo di proiezione le linee parallele restano parallele. Non si conservano invece le misure angolari e i rapporti delle misure.
Gli elementi fondamentali dell'Assonometria sono:
1) Il centro di proiezione posto all’infinito;
2) Le linee di proiezione parallele fra loro;
3) Il piano di proiezione, suddiviso da tre assi cartesiani ortogonali (x, y, z) aventi origine in un punto O.
Gli angoli che questi tre assi formano tra loro (però l'asse z deve essere sempre verticale) determinano i vari tipi di Assonometria e le dimensioni dell’oggetto.
Per determinare sul quadro di rappresentazione la posizione dei punti, è necessario riportarne le coordinate rispetto al sistema di riferimento, seguendo le direzioni assunte dagli assi nella proiezione, e tenendo presenti le variazioni di scala delle misure su tali assi.
A seconda della inclinazione del quadro di rappresentazione (il foglio di lavoro) rispetto ai piani di proiezione (e quindi a seconda degli angoli formati dai tre assi), l'Assonometria può essere OBLIQUA o ORTOGONALE. Ciascuna tipologia di Assonometria è trattata in una pagina a parte di questa sezione.
REALIZZARE UNA ASSONOMETRIA

Una volta stabilita la posizione degli assi assonometrici e i rapporti di riduzione su di essi, è possibile realizzare l'Assonometria. E' importante realizzare prima anche le Proiezioni Ortogonali degll'oggetto da rappresentare, per fissarne la posizione e le misure reali.
Nelle figure piane è sufficiente una "figura preparatoria", cioè la rappresentazione del poligono (in vera grandezza) dato il lato o la circonferenza circoscritta.
Nelle rappresentazioni assonometriche il cerchio viene deformato in un’ellisse. A meno che non sia visto frontalmente in assonometria cavaliera o in pianta nell’assonometria monometrica.
Per rappresentare i poligoni regolari nei vari tipi di assonometria è buona norma procedere per punti (cioè definire la posizione dei suoi vertici), e poi unirli tra loro in modo da formare il poligono.
Saper rappresentare un poligono in Assonometria rende semplice la realizzazione dei solidi (a spigolo o di rotazione). Rappresentato il poligono di base, infatti, sarà sufficiente innalzare le altezze. Anche perchè, qualunque sia il solido assegnato, esso è sempre inscrivibile in un parallelepipedo di riferimento.
Realizzato il solido in Assonometria, occorrerà poi disegnare in linea continua gli spigoli in evidenza, e tratteggiare quelli nascosti.
LA PERCEZIONE DELL'ASSONOMETRIA
Una immagine assonometrica può spesso dare "problemi di percezione".
Questi problemi sono dovuti al fatto che, a causa della loro tridimensionalità, le proiezioni assonometriche forniscono immagini realistiche, che ingannano perciò l'occhio dell'osservatore dando quasi un'idea di "falsa prospettiva".
Nello stesso tempo, però, le proiezioni assonometriche sono frutto di una pura costruzione grafica che nella realtà non esiste. Questo fa sì che si presentino all'occhio di chi guarda come una "strana" prospettiva, nella quale le linee parallele si conservano, anzichè convergere nei punti di fuga.
SPACCATO ASSONOMETRICO E DISEGNO ESPLOSO
Oltre all'Assonometria, di un oggetto è spesso utile disegnare anche lo spaccato assonometrico, nel quale è mostrato l’oggetto in Assonometria come se ne avessimo tagliato una porzione, per poter vedere come è dentro.
Oltre allo spaccato assonometrico è possibile realizzare anche il disegno esploso di un oggetto, utilizzatissimo per rappresentare gli elementi meccanici e le apparecchiature tecniche. Esso è usato per rappresentare e vedere meglio le varie parti che costituiscono un oggetto complesso, staccate dalla parte centrale ma posizionate in modo tale che, che immaginiamo di unire nuovamente le varie parti, si ottiene l’oggetto intero.
TEOREMA DI POHLKE
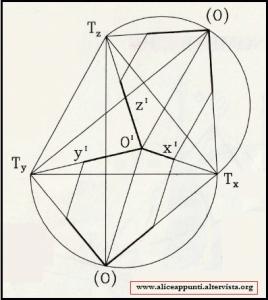
Le proiezioni assonometriche (e in particolar modo quelle a quadro obliquo, chiamate assonometrie ortogonali) si basano sul teorema di Pohlke:
"Tre segmenti uscenti da un punto, con orientamenti e misure qualsiasi, possono comunque rappresentare la proiezione su un quadro da un punto all'infinito di tre segmenti uguali perpendicolari tra loro."
RIPETIZIONI DI DISEGNO TECNICO
SCALE DI RIDUZIONE NELLA ASSONOMETRIA ORTOGONALE
L'appunto (completo e dettagliato) relativo a come determinare le scale di riduzione in assonometria ortogonale e le unità assonometriche è acquistabile qui di seguito, corredato di disegni esplicativi.
NUMERO TOTALE PAGINE: 8
PREZZO APPUNTI: 2,50 Euro
TAVOLE SVOLTE SULL'ASSONOMETRIA NEL DISEGNO TECNICO
ALLA PAGINA "TAVOLE SVOLTE" DELLA SEZIONE DI DISEGNO TECNICO POTRETE VISUALIZZARE UN ESEMPIO DI "ASSONOMETRIA CAVALIERA DI UN EDIFICIO" (TAVOLA 3).







