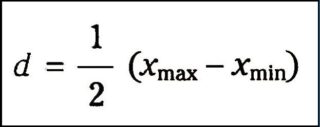In questa lezione vediamo come esprimere la misura di una grandezza generata dal prodotto di altre grandezze, sia per quanto riguarda il valore medio sia per quanto riguarda l’errore commesso. Errore che, naturalmente, deriva da quello delle grandezze di partenza.
INTRODUZIONE:
Nella scorsa lezione (accessibile cliccando qui), abbiamo parlato di come esprimere le misure delle grandezze quand’esse sono frutto della somma o della sottrazione di altre. E abbiamo visto che in quel caso l’errore assoluto è uguale alla somma degli errori assoluti delle grandezze di partenza.
Ma la fisica ci insegna che somma e sottrazione non sono le uniche due operazioni possibili tra le grandezze.
Per esempio, sappiamo che accanto alle grandezze fondamentali (quali lunghezza, tempo, massa…) ne esistono altre, chiamate “grandezze derivate”. Si chiamano così perché si ottengono moltiplicando o dividendo le grandezze fondamentali.
Un esempio tipico è quello della velocità, che non può essere misurata con un comune strumento di misurazione, ma deriva da una lunghezza fratto un tempo.
Quindi ci chiediamo adesso come esprimere la misura di una grandezza generata dalla moltiplicazione di altre.
VALORE MEDIO NEL PRODOTTO DI DUE GRANDEZZE:
Immaginiamo dunque di avere due grandezze affette da errore e di volerle moltiplicare tra loro per determinare il valore di una certa grandezza:
LA = MA ± ∆A
LB = MB ± ∆B
Come si può intuire, MA e MB sono i valori medi delle due misure, mentre ∆A e ∆B sono i loro errori assoluti. Chiamiamo LC la misura della grandezza generata dal loro prodotto.
Il valore medio di LC è facile da calcolare: sarà pari al prodotto dei valori medi di LA e LB.
LC = MC ± ∆C
MC =MA ∙ MB
ERRORE CALCOLATO COME SEMIDISPERSIONE NEL PRODOTTO DI DUE GRANDEZZE:
Vediamo invece quanto vale l’errore. Per calcolarlo utilizziamo il concetto di semidispersione.
Sappiamo che l’errore calcolato come semidispersione prevede l’utilizzazione di questa formula:
Nel nostro caso, LC MAX=LA MAX ∙ LB MAX e LC MIN=LA MIN ∙ LB MIN.
Dove:
LA MAX=MA + ∆A
LA MIN=MA – ∆A
LB MAX=MB + ∆B
LB MIN=MB – ∆B
Quindi:
LC MAX= (MA + ∆A) ∙ (MB + ∆B) = MA ∙ MB + MA ∙ ∆B + ∆A ∙ MB + ∆A ∙ ∆B
LC MIN = (MA – ∆A) ∙ (MB – ∆B) = MA ∙ MB – MA ∙ ∆B – ∆A ∙ MB + ∆A ∙ ∆B
L’ERRORE ASSOLUTO DEL PRODOTTO DI DUE GRANDEZZE:
L’errore calcolato con la semidispersione è pari a:
∆C = ½ (LC MAX – LC MIN) = ½ [(MA ∙ MB + MA ∙ ∆B + ∆A ∙ MB + ∆A ∙ ∆B) – (MA ∙ MB – MA ∙ ∆B – ∆A ∙ MB + ∆A ∙ ∆B)]
Cambiando segno ai termini dentro la seconda parentesi si ottiene:
∆C = ½ (MA ∙ MB + MA ∙ ∆B + ∆A ∙ MB + ∆A ∙ ∆B – MA ∙ MB + MA ∙ ∆B + ∆A ∙ MB – ∆A ∙ ∆B)
Come si vede, alcuni prodotti sono uguali ma di segno opposto, e quindi si eliminano. Sommando tra loro le grandezze rimaste si ottiene:
∆C = ½ (2∙ MA ∙ ∆B + 2∙∆A ∙ MB), e cioè ∆C = MA ∙ ∆B + ∆A ∙ MB
LC = MC ± ∆C
L’errore assoluto è quindi pari alla somma del prodotto del valore medio di una grandezza per l’errore assoluto dell’altra. Definizione, questa abbastanza complicata, e lo diventa ancora di più se le grandezze coinvolte dovessero essere più di due.
L’ERRORE RELATIVO DEL PRODOTTO DI DUE GRANDEZZE:
Vediamo se l’errore relativo ci permette una definizione (e quindi un modo di procedere) più semplice.
Sappiamo che l’errore relativo di calcola dividendo l’errore assoluto per il valore medio della grandezza. Quindi l’errore medio della grandezza LC è pari a: ∆C/MC
Sostituendo a ∆C e ad MC i loro valori, si ottiene che l’errore relativo di LC è pari a:
(MA ∙ ∆A + ∆B ∙ MB)/ MA ∙ MB
Eseguendo la divisione si ottiene: ∆A/ MA + ∆B /MB
Possiamo dunque giungere alla seguente conclusione: l’errore relativo di un prodotto è uguale alla somma degli errori relativi delle grandezze di partenza.
Per ottenere l’errore assoluto, basterà moltiplicare l’errore relativo così trovato per il prodotto dei valori medi delle grandezze di partenza.
GUARDA IL VIDEO DELLA LEZIONE SU YOUTUBE E ISCRIVITI AL MIO CANALE!