In questa pagina vedremo come rappresentare nel disegno tecnico una parabola, in modo da servircene nelle sezioni coniche in proiezioni ortogonali.
CARATTERISTICHE GEOMETRICHE DI UNA PARABOLA:
Una parabola è una curva piana aperta, dotata di un asse di simmetria e di un vertice.
Lungo l’asse di simmetria si trova un punto chiamato “fuoco”. Esternamente alla curva, invece, si trova una retta perpendicolare all’asse, chiamata “retta direttrice”. Retta direttrice e fuoco sono equidistanti rispetto al vertice.
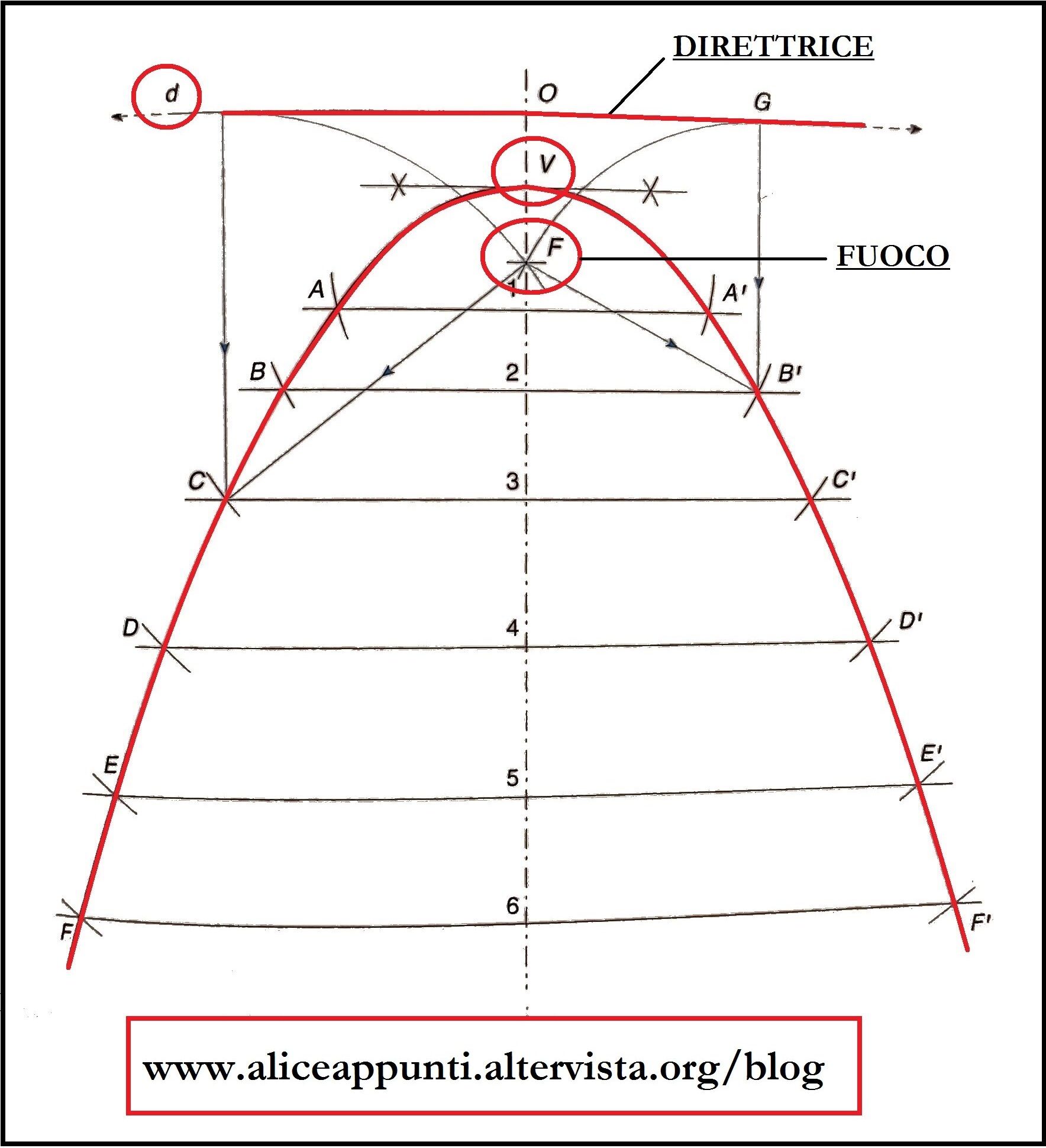
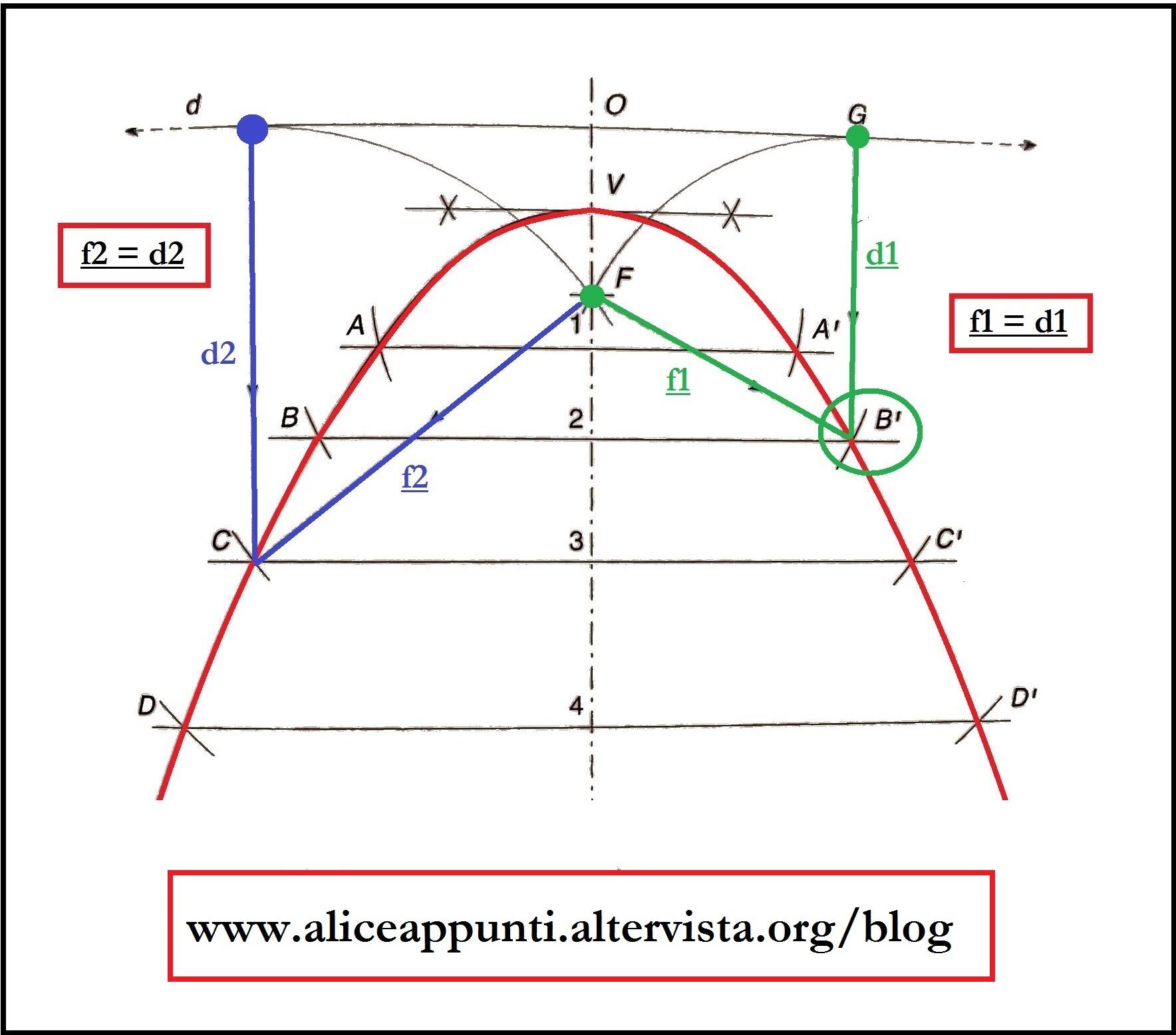
Se prendiamo un qualsiasi punto appartenente alla curva, e calcoliamo la distanza di questo punto da F e dalla retta direttrice, ci accorgeremo che queste due distanze sono uguali. La definizione geometrica della parabola è infatti: luogo geometrico dei punti equidistanti dal fuoco e dalla retta direttrice.
TECNICHE PER COSTRUIRE UNA PARABOLA:
Per tracciare una parabola in disegno tecnico esiste più di un metodo. Alcuni di questi metodi possono essere utilizzati anche per un’altra figura piana: l’iperbole.
Una tecnica che può invece essere utilizzata solo per tracciare una parabola in proiezioni ortogonali è la seguente, chiamata “COSTRUZIONE DATI DUE PUNTI SIMMETRICI E LE RELATIVE RETTE TANGENTI.”
DISEGNARE UNA PARABOLA CON LA COSTRUZIONE DATI DUE PUNTI SIMMETRICI E DUE RETTE TANGENTI:
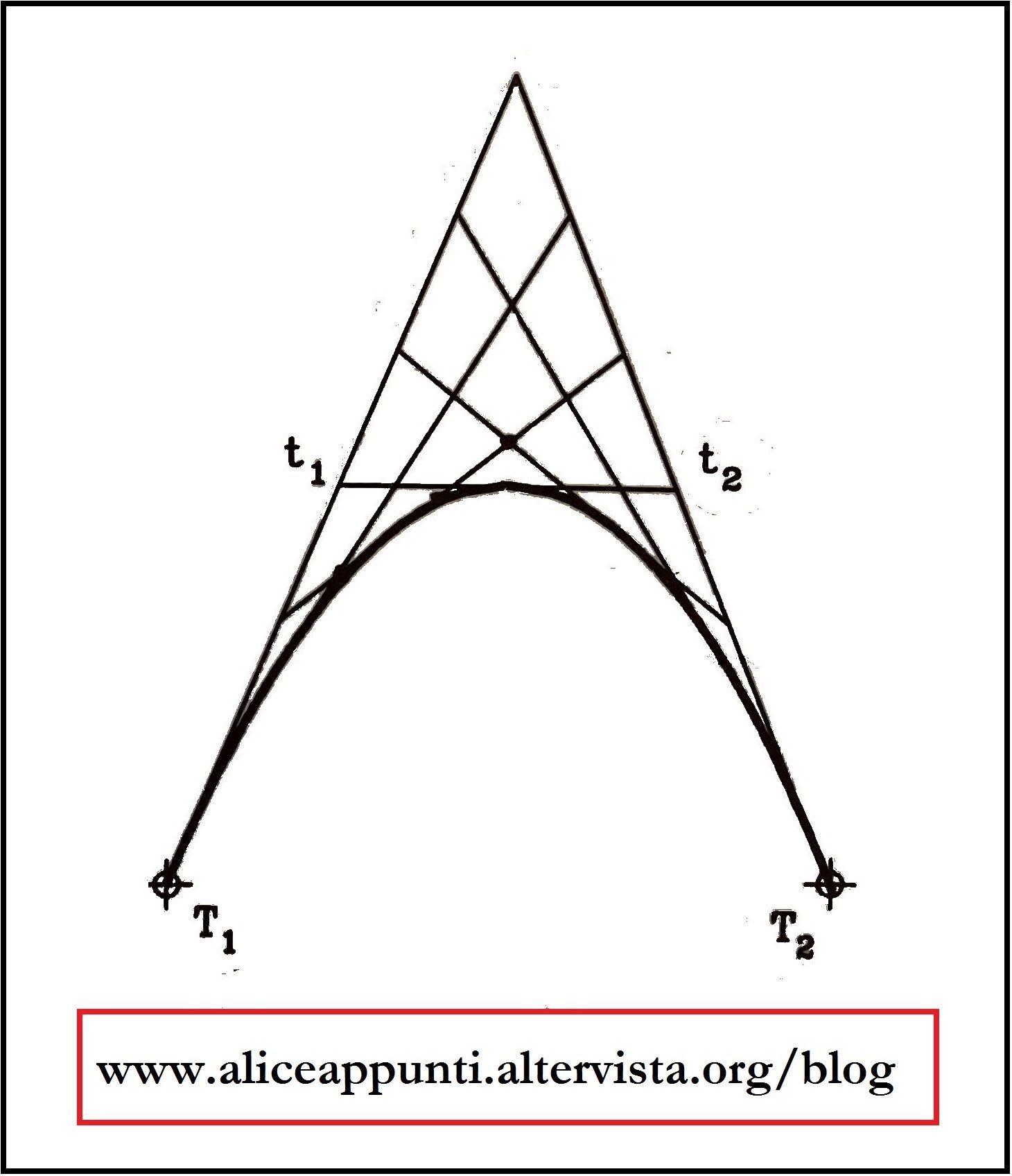
Per poter realizzare la curva con questo metodo, è necessario conoscerne (come ci suggerisce il nome stesso) due punti simmetrici e le due rette tangenti alla curva in quei punti.
Tracciamo l’asse della curva. Essa presenta la seguente caratteristica: la tangente alla curva nel vertice taglia tutte le altre tangenti alla parabola a metà, tra il relativo punto di tangenza con la curva e quello di incontro di esse con l’asse. Questo significa che, se dividiamo a metà le due rette tangenti assegnate, tra il punto in cui sono tangenti alla curva e quello in cui si incontrano, là si troverà la retta tangente alla parabola nel vertice. Più precisamente, il vertice si trova dove questa retta interseca l’asse.
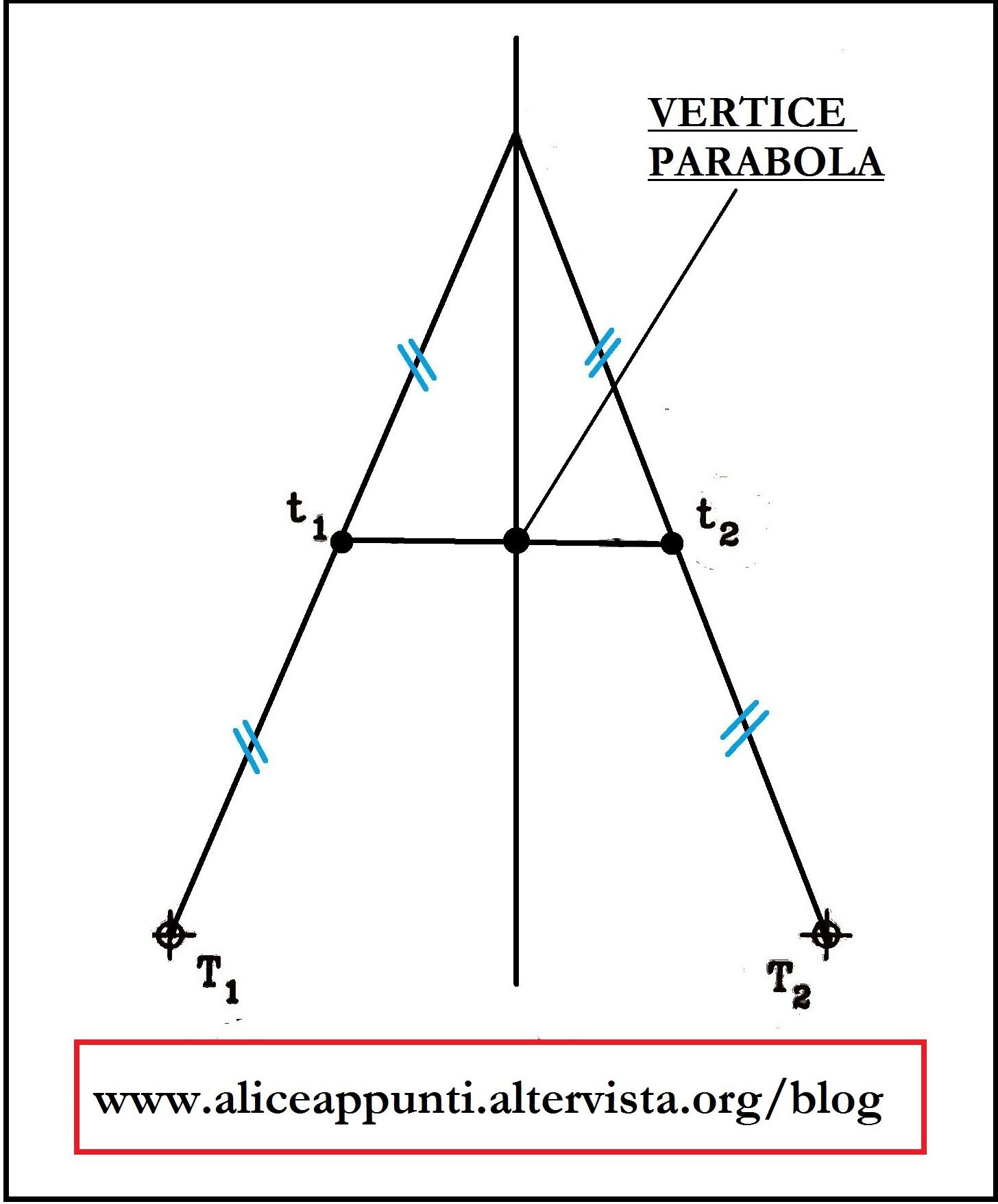
Dividiamo le due tangenti in parti uguali (ad esempio sei, ma potremmo volerne anche di più), e poi uniamo i punti così trovati tra loro.
Le rette tracciate sono delle tangenti alla parabola tra loro simmetriche. Consideriamone due. Misuriamo la distanza che c’è tra il loro punto d’incontro e la retta tangente al vertice della curva. Riporteremo la stessa identica misura al di sotto della retta tangente al vertice. Là avviene la tangenza delle due rette con la parabola. Ripetiamo lo stesso ragionamento anche per le altre tangenti.
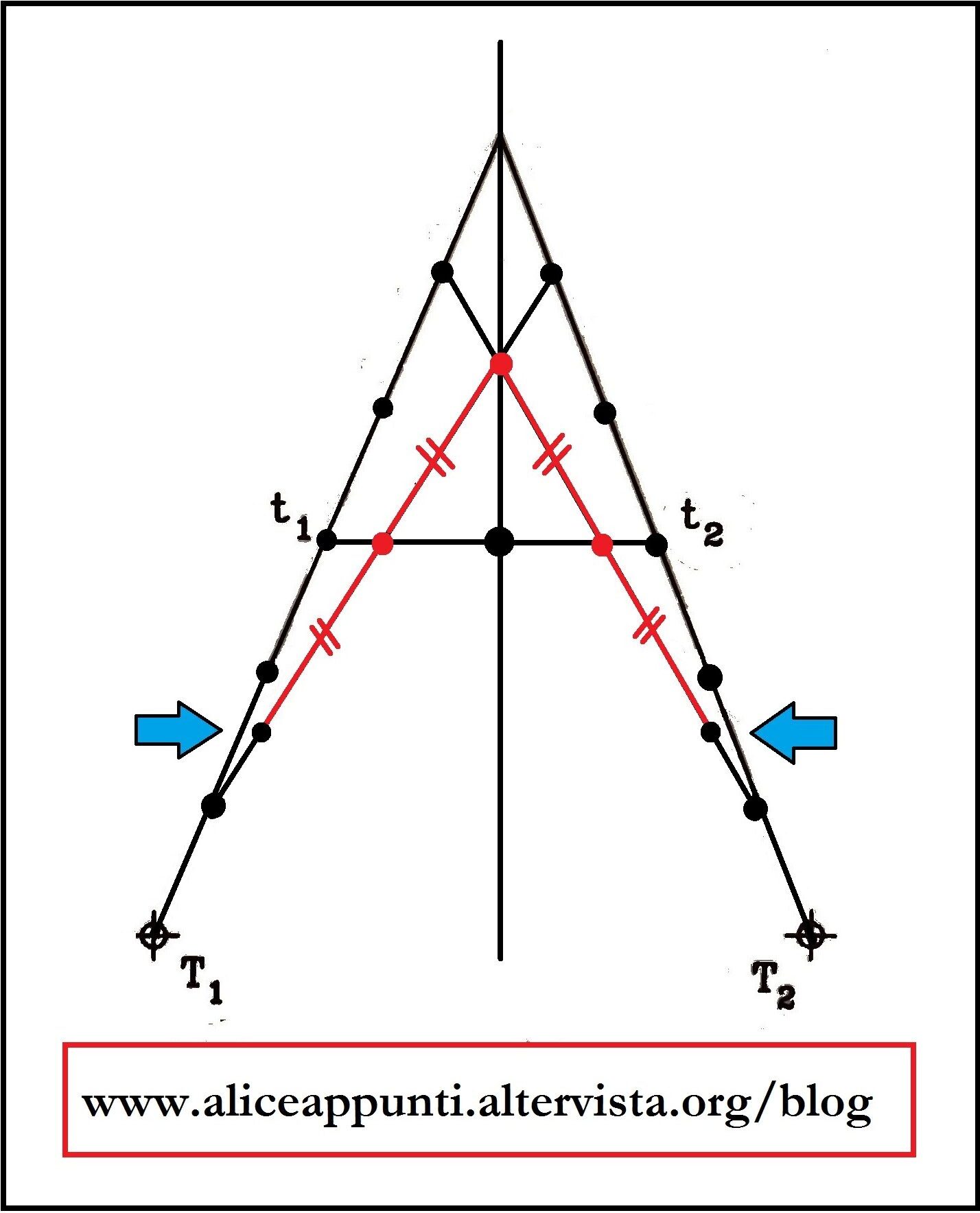
La curva passerà dunque per i punti così trovati. Che uniremo tra loro con il “curvilineo”.
GUARDA IL VIDEO DELLA LEZIONE SU YOUTUBE E ISCRIVITI AL MIO CANALE!
