INTERSEZIONE tra solido e figura piana in proiezioni ortogonali |

In questa lezione vedremo come determinare in proiezioni ortogonali l’intersezione tra un solido e una figura piana. Per esempio tra un parallelepipedo che poggia con la base sul P.O. e un triangolo.

CONSIDERAZIONI PRELIMINARI SULL’INTERSEZIONE TRA IL SOLIDO E LA FIGURA PIANA:

Il triangolo penetra all’interno del parallelepipedo, per poi uscirne. Quindi la parte centrale del triangolo si trova dentro il parallelepipedo, mentre la parte iniziale e finale si trovano fuori.

*Intersezione tra un parallelepipedo e un triangolo. Tratto da: “GEOMETRIA DESCRITTIVA E SUE APPLICAZIONI”, di Saverio Malara. Zanichelli editore.*

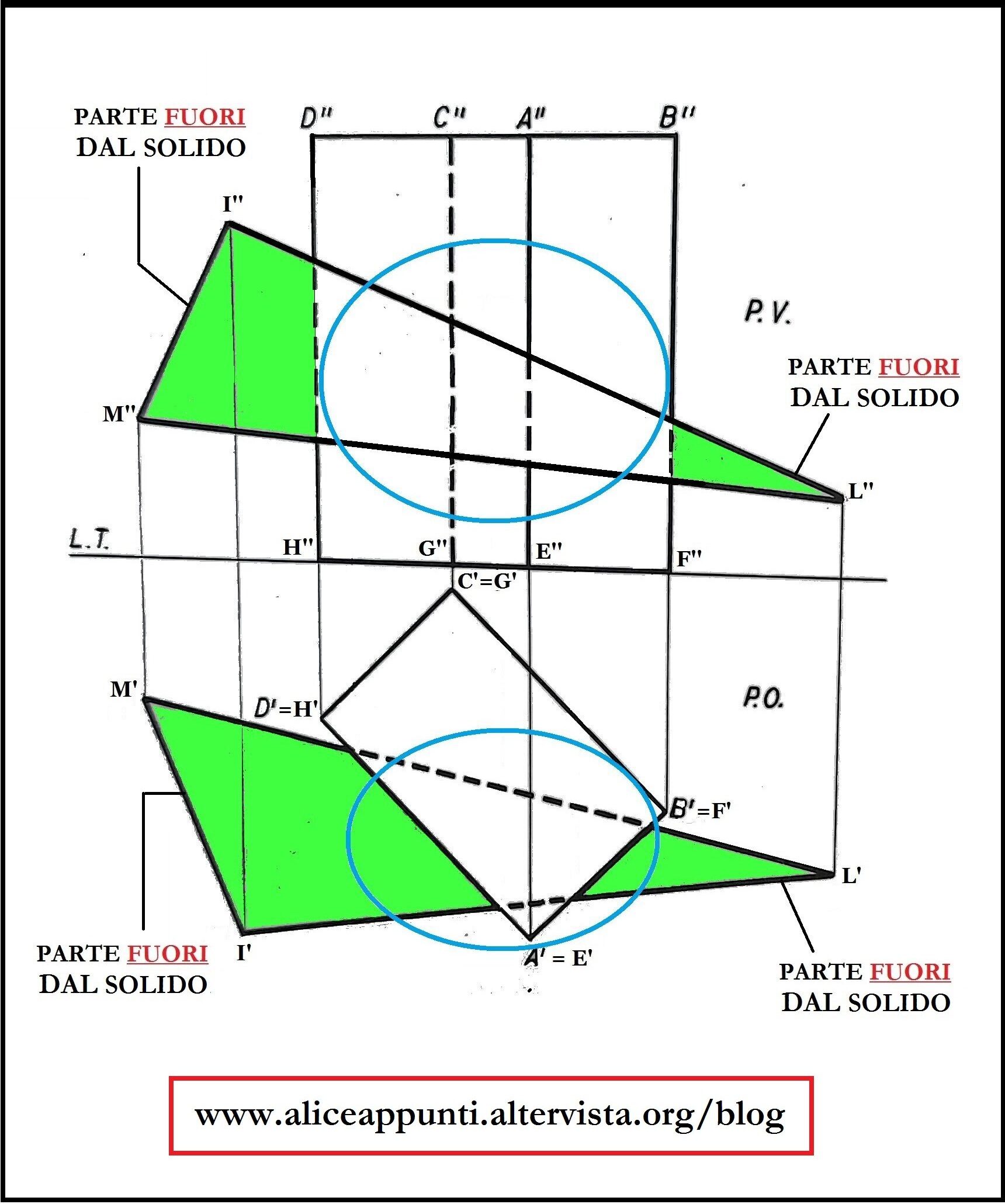
LATI COINVOLTI NELLA INTERSEZIONE TRA IL SOLIDO E LA FIGURA PIANA:

Per prima cosa, notiamo come il lato IM del triangolo non sia coinvolto nell’intersezione. Infatti sia in prima che in seconda proiezione le sue proiezioni non si sovrappongono alle proiezioni ortogonali del parallelepipedo, ma gli sono invece esterne.

I lati IL ed ML, invece, penetrano all’interno del parallelepipedo. Infatti sia in prima che in seconda proiezione le proiezioni dei due lati si sovrappongono alle proiezioni ortogonali del parallelepipedo. Il problema è che non sappiamo quali sono i punti esatti in cui i due lati entrano nel parallelepipedo e quali sono i punti esatti in cui ne escono. Questi quattro punti (due per ciascun lato) si chiamano punti di rottura.

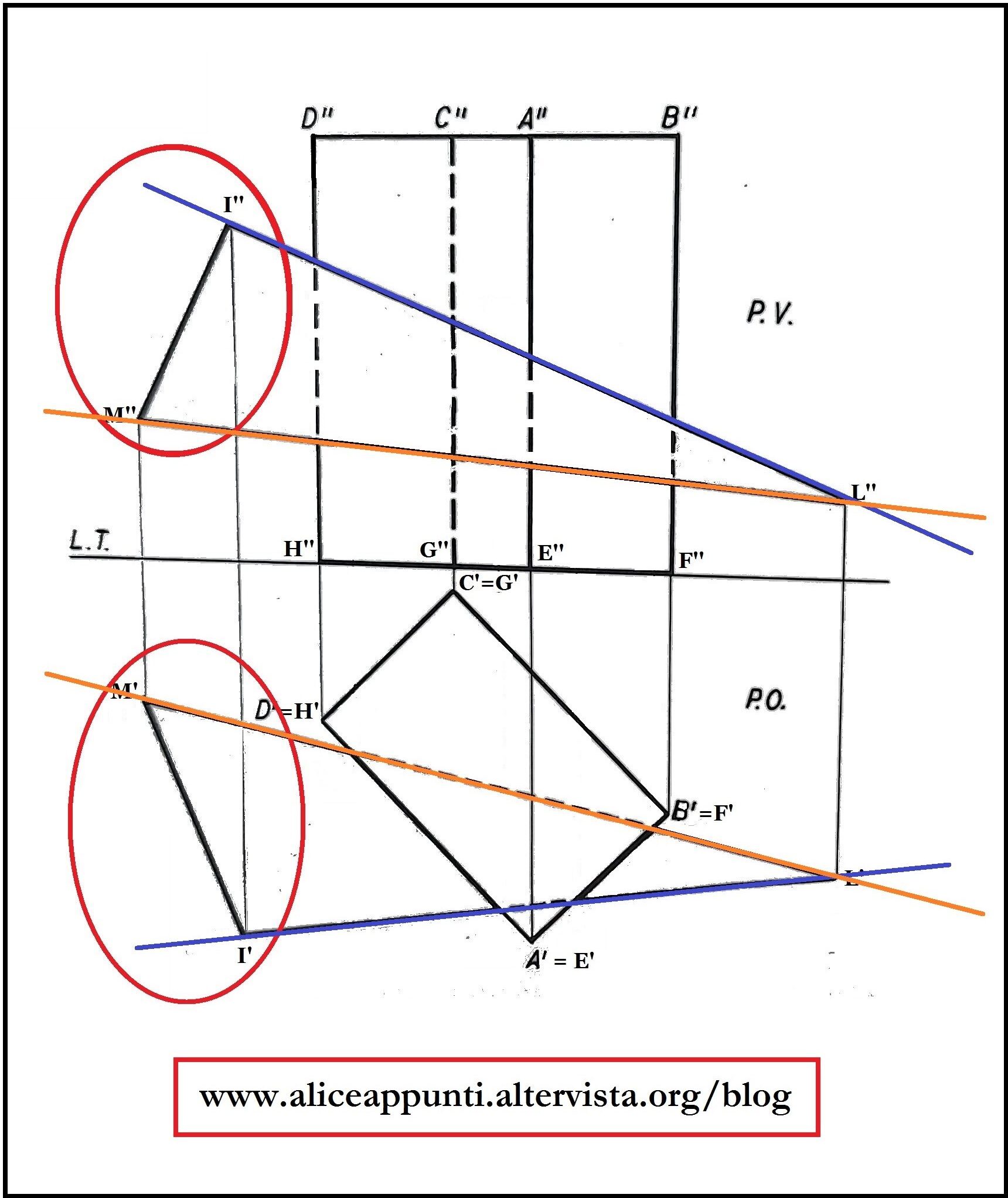
Lati della figura piana coinvolti e non coinvolti nell'intersezione. — *Lati della figura piana coinvolti e non coinvolti nell’intersezione. Tratto da: “GEOMETRIA DESCRITTIVA E SUE APPLICAZIONI”, di Saverio Malara. Zanichelli editore.*

TECNICA UTILIZZATA PER RISOLVERE L’INTERSEZIONE:

L’intersezione tra un solido e una figura piana si risolve in maniera simile a come si risolve l’intersezione tra un solido e una retta. Problema, questo, che abbiamo già trattato nella lezione precedente. Cioè considereremo i lati della figura piana come se fossero rette, e determineremo i loro punti di rottura proprio come si fa nei casi in cui il solido è intersecato fa una retta.

Possiamo decidere di lavorare o in prima o in seconda proiezione indistintamente. In questo caso, lavoreremo per esempio in prima proiezione.

Immaginiamo di passare i due lati (IL ed ML) due piani proiettanti, tali da avere la prima traccia coincidente con ciascuna delle due prime proiezioni dei lati. Questo perché abbiamo deciso di lavorare in prima proiezione. Altrimenti, avremmo fatto passare i due lati due piano proiettante tale da avere la seconda traccia coincidente con ciascuna delle due seconde proiezioni dei lati.

*Piani proiettanti passanti per i lati del triangolo. Tratto da: “GEOMETRIA DESCRITTIVA E SUE APPLICAZIONI”, di Saverio Malara. Zanichelli editore.*

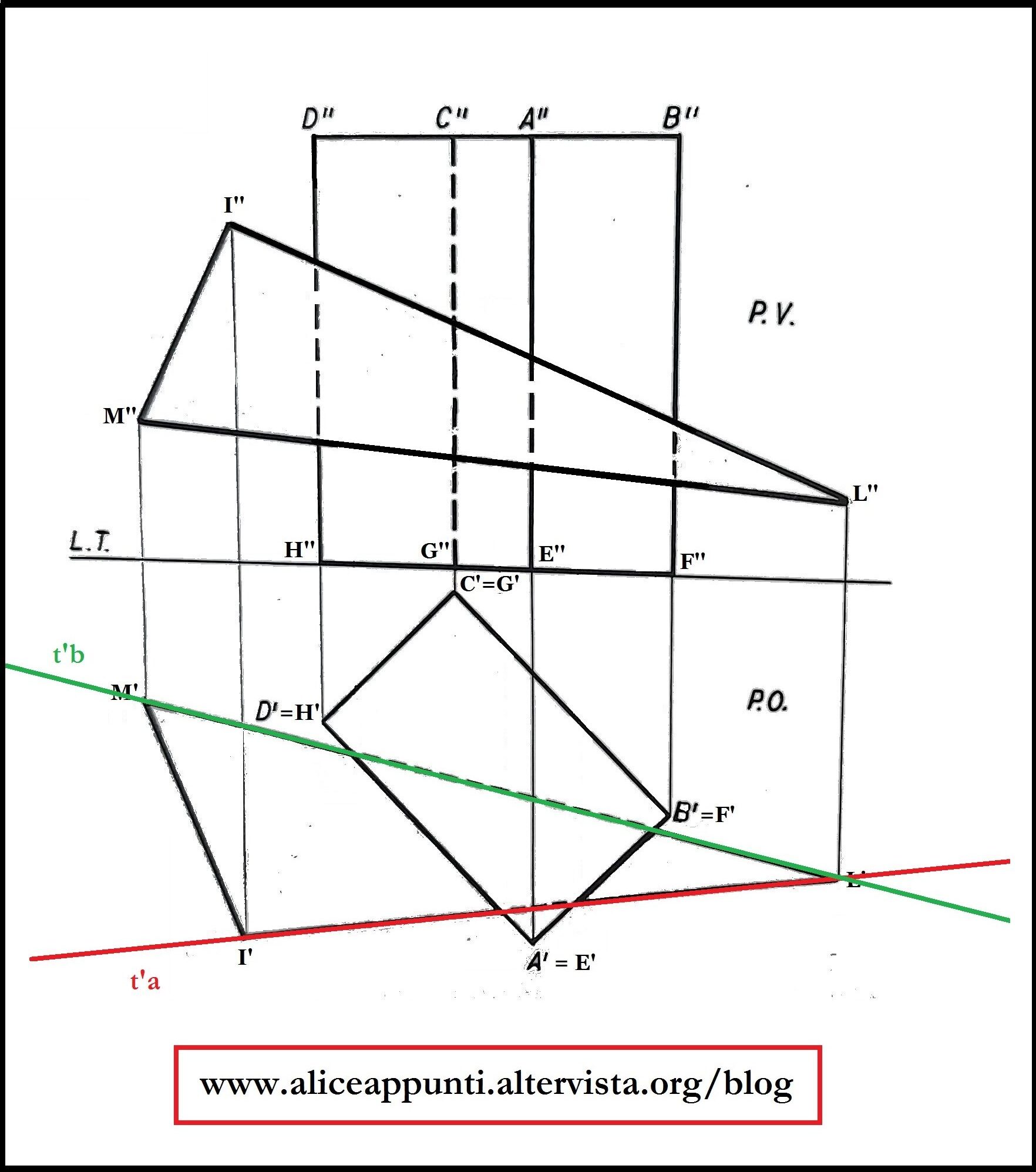
DETERMINAZIONE DELL’INTERSEZIONE TRA IL SOLIDO E LA FIGURA PIANA:

PUNTI DI ROTTURA SUL LATO IL:

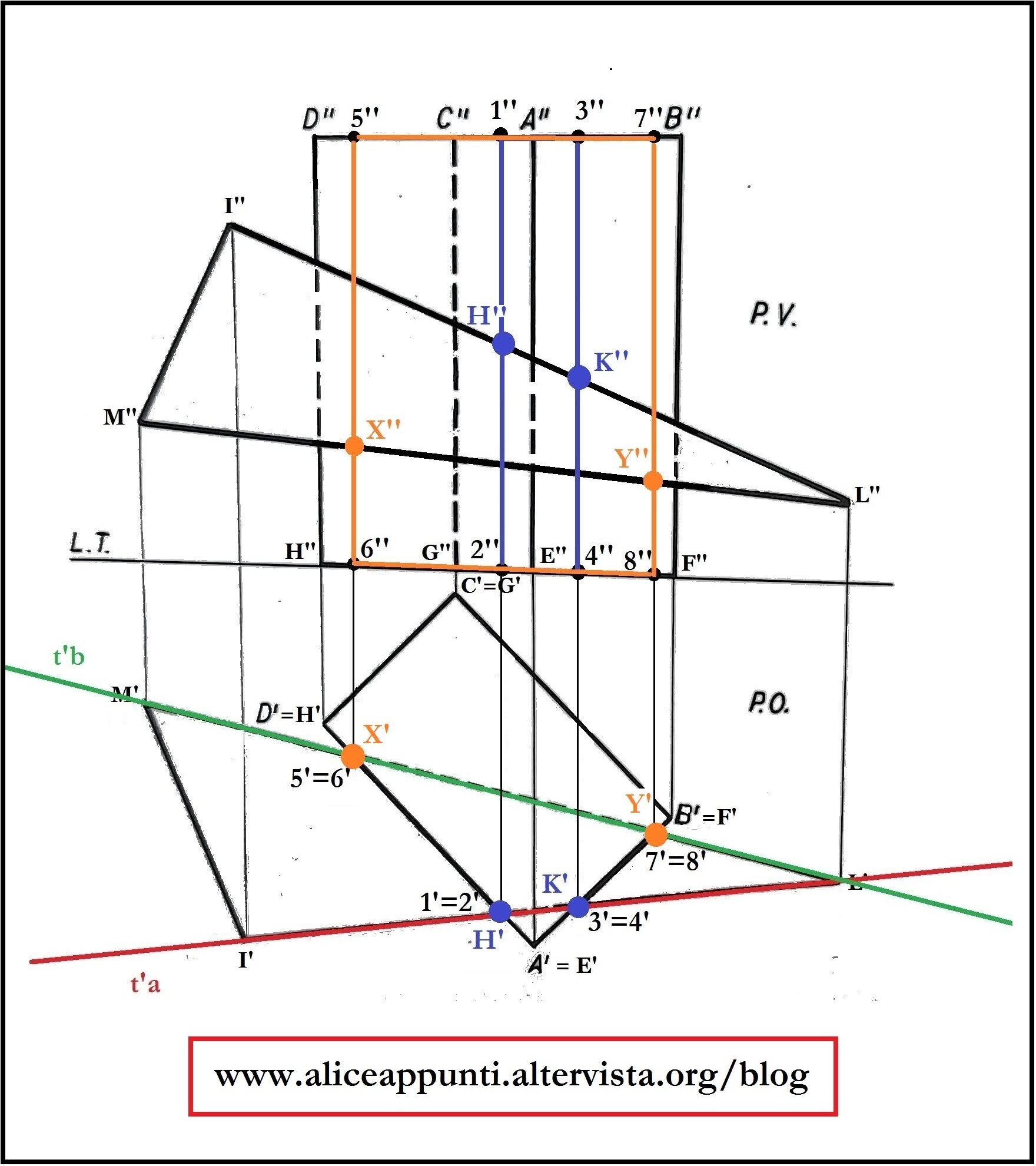
Il piano che passa per il lato I’L’ interseca gli spigoli del prisma in quattro punti a due a due coincidenti: 1’ e 2’ (che si trovano sullo spigolo A’D’ e sullo spigolo E’H’), e 3’ e 4’ (trovano sullo spigolo A’B’ e sullo spigolo E’F’). Riportiamo questi punti in seconda proiezione, attraverso delle rette di richiamo, sugli spigoli corrispondenti.

Questo poligono interseca la seconda proiezione del lato I’’L’’ in due punti, che chiameremo H’’ e K’’. Questi sono i due punti di rottura che stavamo cercando. La parte del lato che si trova all’interno del poligono è la parte che si trova all’interno del solido. Ritroveremo facilmente questi punti in prima proiezione, sullo spigolo I’L’.

*Intersezione tra un solido e una figura piana: punti di rottura sul lato IL. Tratto da: “GEOMETRIA DESCRITTIVA E SUE APPLICAZIONI”, di Saverio Malara. Zanichelli editore.*

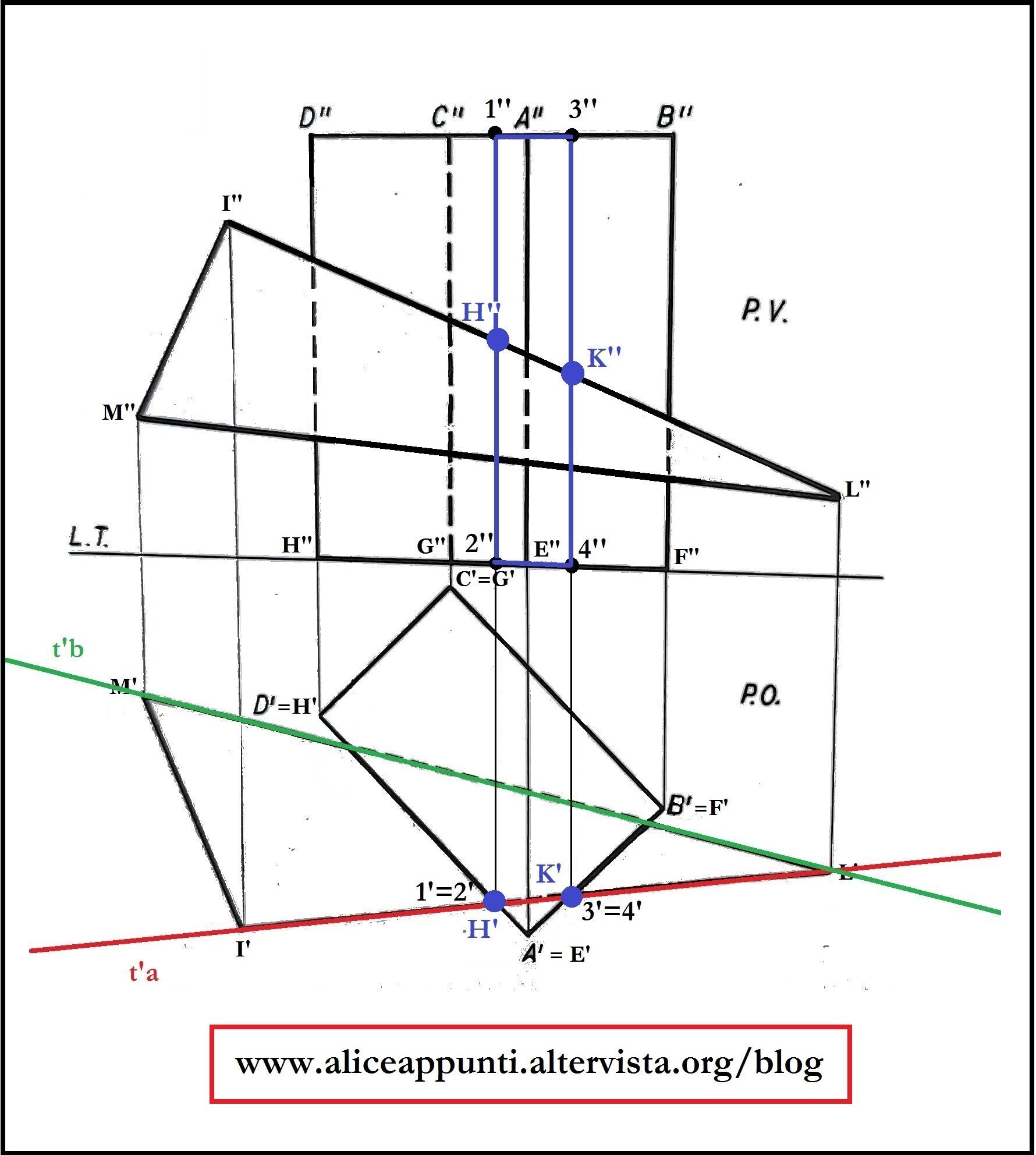
PUNTI DI ROTTURA SUL LATO ML:

Passiamo ora all’altro lato. Il piano che passa per il lato M’L’ interseca gli spigoli del prisma in quattro punti a due a due coincidenti: 5’ e 6’ (che si trovano sullo spigolo A’D’ e sullo spigolo E’H’), e 7’ e 8’ (trovano sullo spigolo A’B’ e sullo spigolo E’F’). Riportiamo questi punti in seconda proiezione, attraverso delle rette di richiamo, sugli spigoli corrispondenti. Uniamo i punti così trovati in modo da ottenere un poligono convesso.

Questo poligono interseca la seconda proiezione del lato M’’L’’ in due punti, che chiameremo X’’ e Y’’. Questi sono i due punti di rottura che stavamo cercando. La parte del lato che si trova all’interno del poligono è la parte che si trova all’interno del solido. Ritroveremo facilmente questi punti in prima proiezione, sullo spigolo M’L’.

CONCLUSIONE DELL’INTERSEZIONE TRA UN SOLIDO E UNA FIGURA PIANA:

*Intersezione tra un solido e una figura piana: punti di rottura sul lato ML. Tratto da: “GEOMETRIA DESCRITTIVA E SUE APPLICAZIONI”, di Saverio Malara. Zanichelli editore.*

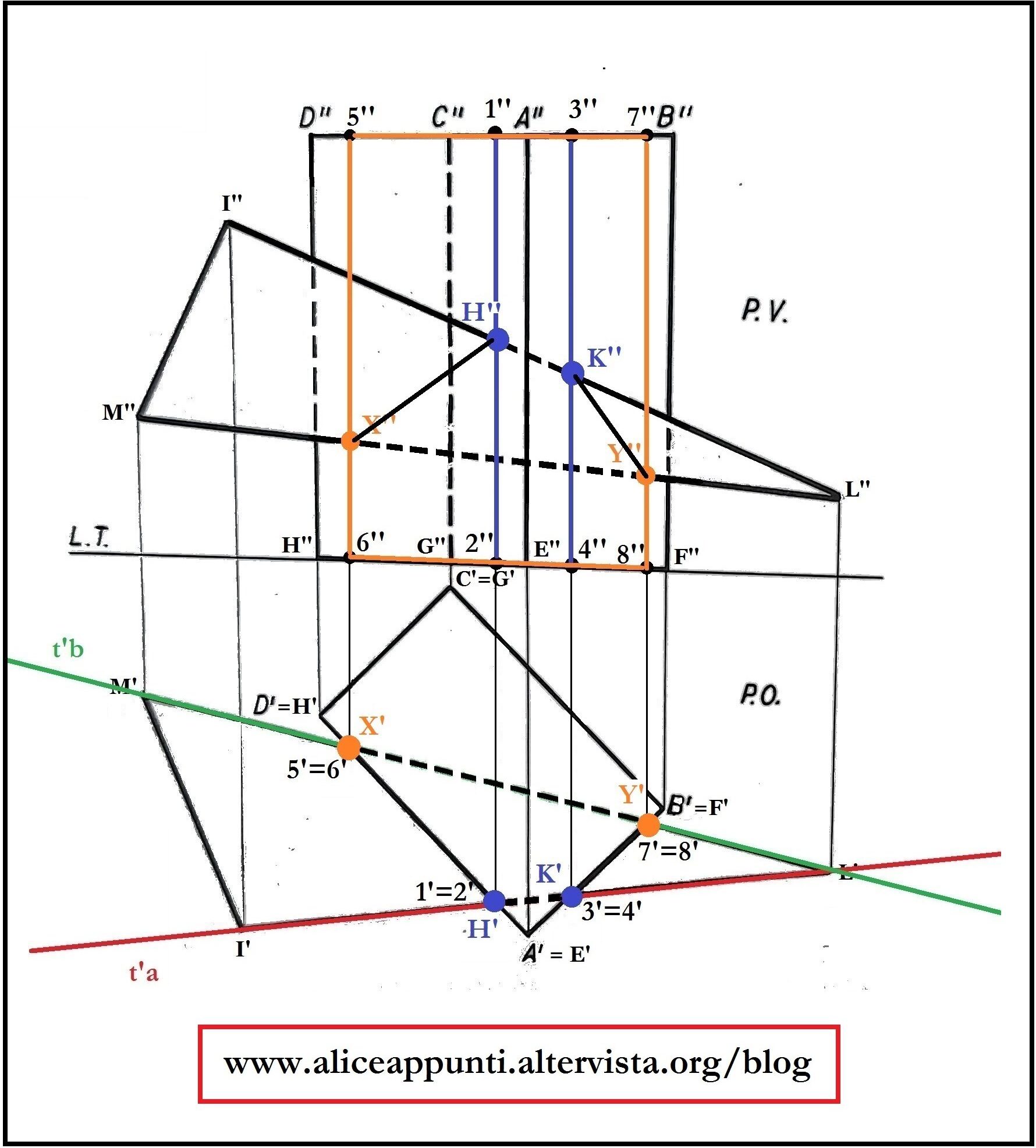
Uniamo tra loro i punti che si trovano sulla medesima faccia del solido, e disegniamo in linea tratteggiata la parte dei due lati del triangolo che si trovano al suo interno.